Sulle cariche negative agisce la forza attrattiva generata delle due cariche positive ![]() e quella repulsiva della carica negativa
e quella repulsiva della carica negativa ![]() .
.
Queste due forze sono agiscono sulla stessa retta (quella che unisce le cariche negative) ma con verso opposto.
Verifichiamo che il modulo sia lo stesso:
![]() è la risultante della somma delle forze
è la risultante della somma delle forze ![]() e
e ![]() delle due cariche positive che formano tra loro un angolo di 120° gradi.
delle due cariche positive che formano tra loro un angolo di 120° gradi.
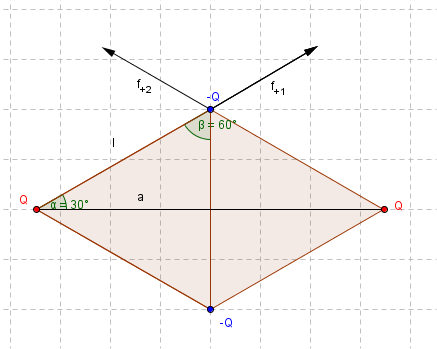
Di queste due forze i componenti paralleli alla sbarretta si annullano, mentre si sommano i componenti perpendicolari, che essendo l’angolo con la perpendicolare di 60° sono pari alla metà di ciascuna forza ![]() e
e ![]()
Pertando sommandosi si ottiene una forza in modulo pari in modulo a una delle due:
![]()
Sempre per i 60° di angolo, inoltre, la distanza l tra ![]() e
e ![]() èpari al lato del triangolo equilatero di altezza a, dunque poiche nel triangolo equilatero
èpari al lato del triangolo equilatero di altezza a, dunque poiche nel triangolo equilatero 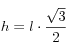
![]()
Dunque
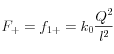
Calcoliamo ora l’espressione di ![]() ; la distanza tra le cariche negative è sempre il lato l del triangolo equilatero di altezza a.
; la distanza tra le cariche negative è sempre il lato l del triangolo equilatero di altezza a.
Dunque:
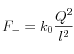
Essendo le due forze ![]() e
e ![]() uguali in modulo e opposte in verso la risultante delle forze è nulla.
uguali in modulo e opposte in verso la risultante delle forze è nulla.
In aggiunta: calcolate ora l’espressione della forza risultante agente sulle cariche positive.
